How To Change Slope Intercept Form Into Standard Form

Slope Intercept Grade Figurer

Created past Álvaro Díez and Bogna Szyk

Reviewed by

Dominik Czernia , PhD candidate and Jack Bowater

Concluding updated:

December 05, 2021

Tabular array of contents:

• What is the slope intercept grade?
• Slope intercept formula derivation
• How to detect the equation of a line?
• Find the x-intercept and y-intercept
• Existent earth uses of y-intercept and ten-intercept
• Other equations with y-intercept
• Equations with no intercept (asymptote)
• Intercepts and linear equations in auto learning and science

The slope intercept form computer will teach yous how to find the equation of a line from any two points that this line passes through. It volition help you lot to find the coefficients of slope and y-intercept, as well every bit the x-intercept, using the gradient intercept formulas. Read on to learn what is the gradient intercept form of a linear equation, how to detect the equation of a line and the importance of the slope intercept class equation in real life.

What is the slope intercept class?

Any line on a flat plane tin can be described mathematically equally a relationship betwixt the vertical (y-axis) and horizontal (x-axis) positions of each of the points that contribute to the line. This relation can be written every bit y = [something with 10]. The specific form of [something with x] will decide what kind of line we accept. For instance, y = 10² + x is a parabola, likewise called a quadratic function. On the other paw, y = mx + b (with m and b representing whatever real numbers) is the relationship of a direct line.

source: Wikimedia

In this slope intercept estimator, we will focus simply on the straight line, but those interested in knowing more almost the parabolic function should non worry. We accept two special calculators dedicated to such an equation, namely the parabola calculator and the quadratic formula calculator. There you tin discover a full clarification of these types of functions! You can likewise bank check our boilerplate rate of change figurer to notice the relation between the variables of non-linear functions.

Linear equations, or directly line equations, tin be apace recognized equally they have no terms with exponents in them. (For example, yous will find an 10 or a y, but never an 10².) Each linear equation describes a straight line, which tin can be expressed using the gradient intercept course equation.

As we have seen earlier, you can write the equation of any line in the class of y = mx + b. This is the so-chosen slope intercept grade considering it gives yous two of import pieces of information: the slope thou and the y-intercept b of the line. Y'all tin can apply these values for linear interpolation afterward.

The term slope is the incline, or gradient, of a line. It tells us how much y changes for a fixed change in 10. If it is positive, the values of y increase when x increases. If it is negative, y decreases with an increasing x. You lot can read more than about it in the description of our slope calculator.

The y-intercept is the value of y at which the line crosses the y-axis. To find it, yous have to substitute 10 = 0 in the linear equation. You will see later, why the y-intercept is an important parameter in linear equations, and you volition also learn nearly the physical meaning of its value in certain real-world examples.

Slope intercept formula derivation

Nevertheless demand to know how to notice the gradient intercept form of a linear equation? We will assume you know 2 points that the straight line goes through. The first one will have coordinates (x₁, y₁) and the second i (x₂, y₂). Your unknowns are the slope k and the y-intercept b.

Firstly, substitute the coordinates of the ii points into the slope intercept equation:

(i) y₁ = mx₁ + b

(2) y₂ = mx₂ + b

And so, decrease the first equation from the 2nd:

y₂ - y₁ = grand(x₂ - x₁)

Finally, divide both sides of the equation by (x₂ - ten₁) to discover the slope:

m = (y₂ - y₁)/(x₂ - 10₁)

Once yous accept found the slope, y'all tin can substitute information technology into the showtime or second equation to find the y-intercept:

y₁ = 10₁(y₂ - y₁)/(10₂ - x₁) + b

b = y₁ - ten₁(y₂ - y₁)/(10₂ - x₁)

How to observe the equation of a line?

This gradient intercept class calculator allows you to notice the equation of a line in the slope intercept form. All you have to do is requite two points that the line goes through. You lot demand to follow the process outlined below.

1. Write down the coordinates of the first indicate. Let'southward assume it is a point with x₁ = one and y₁ = one.

2. Write down the coordinates of the second point as well. Let's accept a point with x₂ = 2 and y₂ = 3.

3. Utilize the slope intercept formula to find the slope:

   • m = (y₂ - y₁)/(x₂ - ten₁) = (3-1)/(2-1) = 2/1 = ii.

4. Calculate the y-intercept. You tin can also use 10₂ and y₂ instead of x₁ and y₁ here.

   • b = y₁ - k * ten₁ = i - 2*1 = -i

5. Put all these values together to construct the slope intercept form of a linear equation:

   • y = 2x - 1.

6. Yous tin besides use the distance calculator to find the altitude between ii points.

Find the x-intercept and y-intercept

It is besides always possible to notice the x-intercept of a line. It is the value of x at which the directly line crosses the x-axis (it means the value of x for which y equals 0). You can summate it in the post-obit way:

0 = mx + b x = -b/g

Our slope intercept form calculator will display both the values of x-intercept and y-intercept for you.

Real globe uses of y-intercept and x-intercept

We have already seen what is the slope intercept form, only to empathise why the slope intercept class equation is so useful you should know some applications information technology has in the real world. Let'due south see a couple of examples. We will beginning with unproblematic ones from physics so that you can get an intuitive idea of what the y-intercept and x-intercept hateful.

Imagine a car moving at a fixed speed towards you. Its movement can be plotted as time versus the altitude the car is from you lot (every bit shown above). This means that the ten-axis will correspond the time passed, and the y-axis will stand for the distance to the car. You lot tin fifty-fifty imagine the car has started to motion earlier you started the timer (that is: before t = 0).

Now, if you await at the y-intercept (ten = 0), the signal at which yous started to go on track of time is t = 0. And so, the value of y at this point will indicate the starting position (distance) of the car with respect to you. This value is, like we have discussed before, the same every bit the value of b in the slope intercept form of a directly line equation.

Looking now at the x-intercept (y = 0), this will exist the point at which the distance from the car to you volition be 0. And then the value of 10 at this point volition be the time when you and the car were at the aforementioned place. Let's hope that means you lot were inside the automobile, and not under.

Other equations with y-intercept

The motorcar instance above is a very unproblematic one that should help y'all understand why the slope intercept form is important and, more than specifically, the meaning of the intercepts. In this commodity, we will mostly talk about directly lines, merely the intercept points tin can be calculated for any kind of curve (if it crosses an axis).

In fact, the example above does non fit a linear equation and still has both intercepts. The same is true for any other parabola or other shape.

One equation that is guaranteed to have a y-intercept but not necessarily an ten-intercept is a parabola. This is equation is shown in the image above. It has a maximum or a minimum (depending on the orientation). If this maximum is below the x-axis or the minimum is above the ten-axis, there will never be an x-intercept.

Even so, unlike humans, not all equations are equal. Some of the formulas describe curves that might never intercept the ten-axis, or the y-axis or both. Let's see in a fleck more detail how this tin be.

Equations with no intercept (asymptote)

We tin can distinguish three groups of equations depending on whether they have a y-intercept only, an x-intercept simply or neither. The kickoff group (y-intercept only) can have almost whatever type of equation, including linear equations. A good piece of cake case is y = 3 (or any other abiding value of y except for 0) since this is a line parallel to the x-axis and will, thus, never cross or intercept it. Please don't try to calculate these types of intercepts on this slope intercept class calculator equally these types of equations can potentially break the Net.

The second and 3rd group of equations are a bit more catchy to imagine, and to understand them well we need to introduce the concept of an asymptote. An asymptote is a line (that can exist expressed equally a linear equation) to which the function or bend we are talking about gets closer and closer to, but never actually crosses or touches that line.

The definition might not seem totally clear but if we await at an instance equation we will have fewer problems with understanding information technology. Allow's take the equation y = ane/x. If we effort to notice the y-intercept by substituting x = 0 nosotros get in at what is called a mathematically undefined expression since it makes no sense to dissever by 0.

If we take values closer and closer to 0 (something like 0.1, then 0.001, 0.000001...) we can meet that the value of y increases very speedily. And so around the point x = 0, we know that y would accept a massive value, simply because of how math works information technology does non have a divers value for that exact bespeak. Sometimes people may say one/0 = ∞ but the reality is that infinity is non a number but a concept.

In this case, the linear equation ten = 0 represents the asymptote of the office y = one/10 which means that y = 1/x will never intercept that line, and thus will non take a y-intercept. In general, any time that a function has an asymptote that lies on one of the axes, information technology will exist missing at to the lowest degree i of the intercepting points.

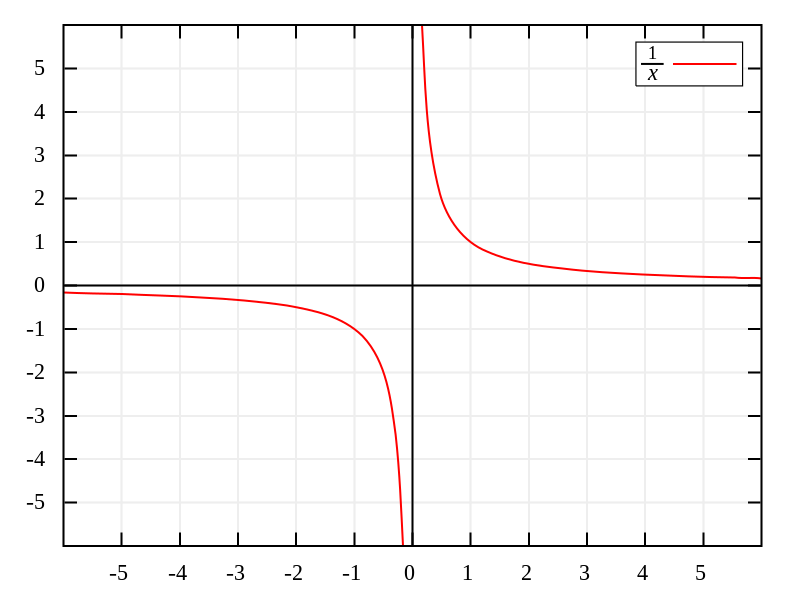
A plot of the hyperbola y = 1/ten (source: Wikimedia).

In fact, the example we have shown y'all (y = 1/x) also has an asymptote for y = 0, i.e., the x-axis. For the same reason as before, y = 0 is never achievable by the formula considering it would require x = ∞ and as we said earlier, it is impossible to achieve that since infinity is a concept and not a number.

Before we move to our next topic, it is important to notation that we accept made extreme over-simplifications when talking about infinity, merely we experience it is a good and fast arroyo for those that are non used to the concept of working with infinity in math. We recommend that you learn more than about the proper ways of the infinity, starting with the undefined expressions in math.

Intercepts and linear equations in machine learning and science

1 could easily recollect that the usefulness of linear equations is very limited due to their simplicity. However, the reality is a bit different. Linear equations are at the cadre of some of the virtually powerful methods to solve minimization and optimization problems.

Minimization issues are a type of problem in which one would similar to notice how to brand one of the variables as small as possible. This variable could be, for case, the difference between a prediction made past a model and the reality. These types of issues are i of the most mutual bug and are at the core of machine learning and scientific experiments.

I of the about common and powerful methods to find the minimum value of an equation or formula is the so-called Newton method, named later on the genius that invented it. The manner it works is by using derivatives, linear equations, and x-intercepts:

Example of using the Newton method (Wikimedia).

This method consists of choosing a value of 10 for the equation and calculating the derivative of the equation at that point. Using the derivative as the slope of a linear equation that passes through that verbal (x, y) betoken, the ten-intercept is so calculated. This is ane of the situations in which the slope intercept grade comes in handy.

One time the x-intercept is calculated, that value of x is used to repeat the procedure above, a specific number of times, until we arrive at a value of y that is minimum (which ways that the derivative will be 0). In real life, arriving at the exact minimal signal is not possible to do in a finite corporeality of fourth dimension, and then typically people will settle for a "shut enough" value.

One very common example is when using the chi-foursquare method to fit some information to a formula or tendency. In this case, the value that we want to minimize is the sum of the squared distanced from the tendency line to the data points, where the distance is calculated along a perpendicular line from the point to the trend line.

Álvaro Díez and Bogna Szyk

Slope intercept form: y = mx + b

Average rate of change Bilinear interpolation Catenary curve … 32 more

Source: https://www.omnicalculator.com/math/slope-intercept-form

Posted by: fosdickgagainfoute.blogspot.com

Share this post